General Motivation

One prerequisite for accurate forces in classical molecular dynamics (MD) simulations is the proper treatment of electrostatic interactions. An accurate representation of these is especially important for the simulation of ions and molecules in solvation and confinement, where polarization and charge transfer effects play a significant role. While these are impossible to reproduce with conventional force fields (FFs), which often use a static point charge approach, methods have been developed to construct polarizable FFs.

One well established example is the electronegativity equalization method (EEM) developed by Mortier et al., in which the electronic energy is expressed as a quadratic function of the atomic charges. Solving the system of linear equations (SLE) that arises when minimizing this expression yields these charges for a given molecular geometry. Within EEM, atomic charges can fluctuate and respond to structural alterations, yet EEM has inherent shortcomings, as it tends to overestimate charge transfer effects, often falsely imposing conductor-like behavior. In the same vein, EEM predicts cubic rather than the expected linear scaling of the dipole polarizability with system size and does not yield proper integer charges upon dissociation of molecules.

Verstraelen et al. addressed these shortcomings by first developing an atom-condensed density functional theory (DFT) formalism which they used to rigorously derive EEM from the Hohenberg-Kohn formulation of DFT, taking note of every approximation introduced along the way. Thus they identified the source of the above-mentioned weaknesses of EEM as the semi-local approximations made for the exchange, correlation, and most severely, kinetic contributions to the total energy. By applying their atom-condensed formalism to the Kohn-Sham formulation of DFT and expanding the kinetic contribution to second-order Verstraelen et al. then derived the energy expression for the new and aptly named atom-condensed Kohn-Sham DFT approximated to second order (ACKS2) model, which is free of the shortcomings of EEM regarding dipole polarizability scaling and dissociation limits.

ACKS2 Energy Expression

The ACKS2 energy expression Verstraelen et al. derived is formally an extension of EEM by their new kinetic energy model:

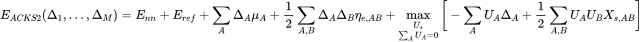
is the nuclear repulsion energy, is the reference energy of the second-order expansion and are the atomic populations, which are equivalent to the atomic partial charges , assuming a neutral reference state. and are the well-known expansion coefficients of EEM, namely the atomic chemical potentials and atomic ( ) and off-diagonal ( ) hardnesses. The points of reference for the new kinetic model are the relative atomic Kohn-Sham potentials , whereas the expansion coefficients are the non-interacting (or Kohn-Sham) linear responses .

The minimum of the ACKS2 energy is a stationary point of the following Lagrangian, where the total charge is constrained to zero:

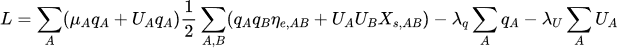
Setting the derivatives of with respect to , , and the Lagrange multipliers and to zero leads to the following system of linear equations (SLE):

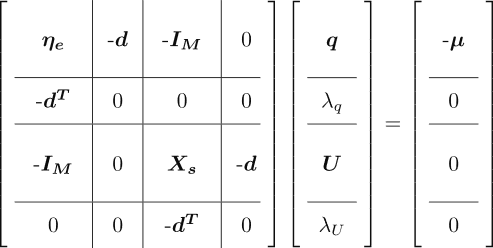
Here, is the identity matrix of size and is an all-ones column vector. Solving this SLE yields the atomic partial charges in the ACKS2 ground state, given the knowledge of , , and . These are the ACKS2 parameters.

Current Progress

• Parameterization strategy for ACKS2 (and EEM) parameters developed and fully implemented in python.

• MOF-FF-compatible ACKS2 implementation added to LAMMPS, based on implementation by Aktulga et al. for ReaxFF.

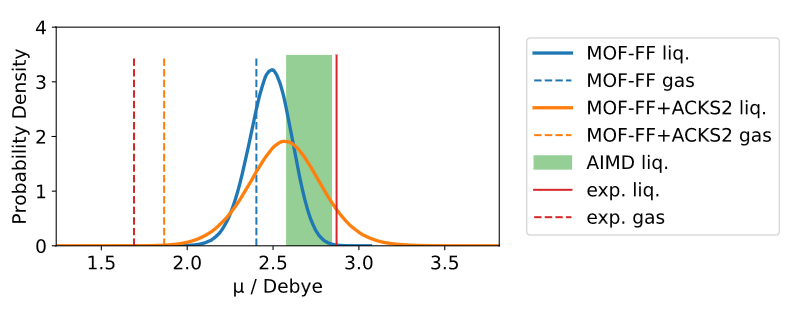
• Fully parameterized polarizable MOF-FF+ACKS2 model for methanol developed, where the effect of ACKS2-augmentation on dipole distribution in MD simulations is well observable:

Long term goals

• Expansion of optimized ACKS2 parameter database

• Development of polarizable FFs for MOFs to study confinement effects