Generalities

The aim of the RSDFT project is to perform standard Kohn-Sham-DFT calculations and molecular dynamics simulations by using real space discretized wavefunctions (ψ(r)) and densities (ρ(r)) within the Car-Parrinello (CPMD) approach [1, 2]. As it is well known, in such scheme the self-consistent cycle to obtain the converged Born-Oppenheimer (BO) Kohn-Sham ground states (KS-GS) for each atomic configuration ({ }) is replaced by an electron fictitious dynamics such that the KS-GS single-particle wavefunctions oscillate around the corresponding BO states. The key ingredient of the CPMD is the extended Lagrangian:

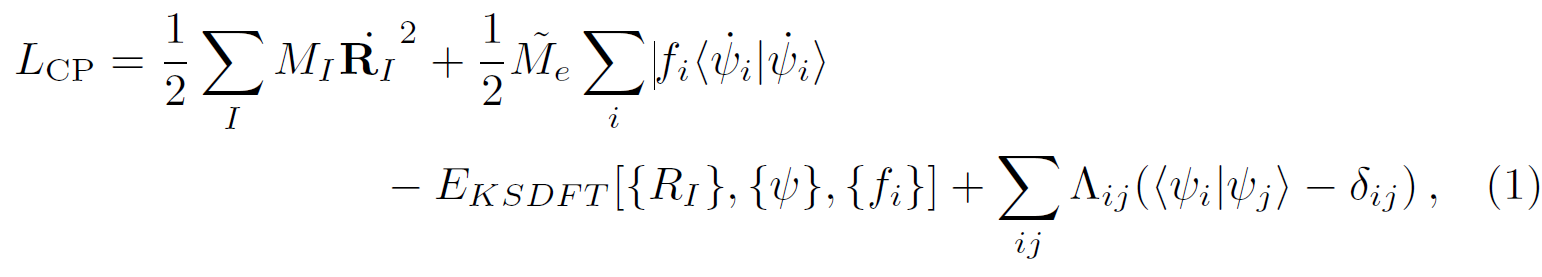
where the first two terms are the nuclear and fictitious electron kinetic energies, respectively, is the usual KS density functional and enforces the orthonormality constraints of the wavefunctions. In RSDFT the dynamics (free or damped) is done by a second-order position verlet-scheme, while orthonormality is achieved by using the standard SHAKE algorithm. In turn, operators acting on wavefunctions and densities are approximated by finite difference (FD) operators, in particular, the Laplacian of the true kinetic electronic energy and in the Poisson equation used for the evaluation of the Hartree energy ( ):

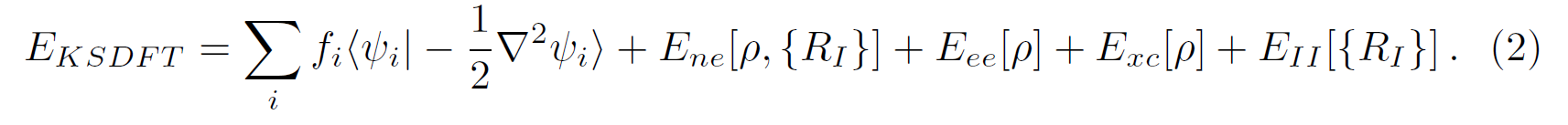
Finally, electron-nuclei interaction are described by norm-conserving pseudopotentials in the KB form and exchange-correlation (XC) functionals up to the GGA level.

Coding Details

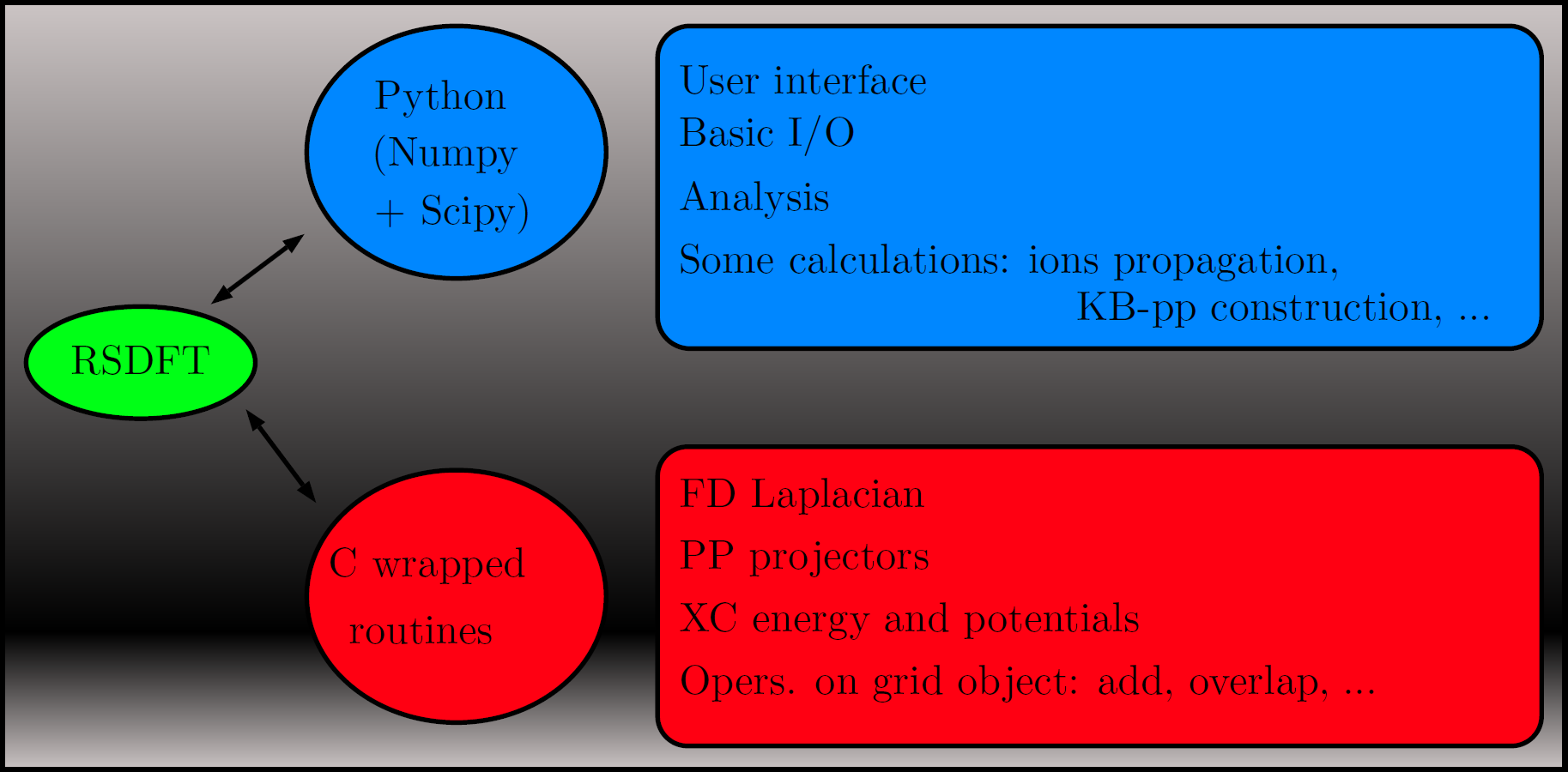
The full prototyping environment of RSDFT is developed in Python using wrapped C routines for the computationally expensive parts. Thus, tasks like input parsing, control flow or analysis, and even ions time propagation, are done in Python, while the FD-Laplacian, XC-energies and pseudopotential projectors are done in C. The main objects in RSDFT are wavefunctions, densities and potentials represented as sets of 3D cartesian equidistant meshes. Such grids are are distributed over nodes in a parallel run and can be scaled, added, differentiated, integrated or overlaped by suitable methods. At the Python level, array operations are handled by the Numpy module and, in general, optimized linear algebra packages (BLAS, LAPACK) are called by the methods operating on grids.

Features

• Ab-initio MD: CPMD, NVE, NVT, Metadynamics.
• Free and damped second-order dynamics.
• Boundary conditions for finite, extended (3D) and 2D periodic (charged) systems.
• High order FD Laplacian (19 point stencil).
• Norm-conserving pseudopotentials (interface to FHI98pp and APE) with fully non-local KB separation.
• Fourier filtering of PPs.
• Multigrid Poisson solver for the Hartree potential.
• Poisson solver for non-constant dielectric permitivities (on development).
• XC functionals up to GGA rung (interface to Libxc).
• Dispersion-corrected DFT (interface to DFT-D2 and DFT-D3)
• CPMD including unoccupied states (suitable SHAKE algorithm).
• CPMD for semiconductors at finite temperature, metals and zero gap systems (on development).
• CPMD at constant chemical potential (on development).

References

• [1] Schmid R., Car-Parrinello simulations with a real space method, Journal Computational Chemistry 25, 1096 (2004).
• [2] Schmid R., Tafipolsky M., König P. H. and Köstler H., Car-Parrinello molecular dynamics using real space wavefunctions, Physica status solidi (b) 243, 1521 (2006).